哈希技术

布隆过滤器

• $k$：哈希函数个数
• $m$：位数组大小
• $n$：元素个数
• $\epsilon$：误判率

最优的位数组大小

$$m = 1.44nlog_2\frac{1}{\epsilon}$$

最优的哈希函数个数

$$k = ln2 \cdot \frac{m}{n}$$

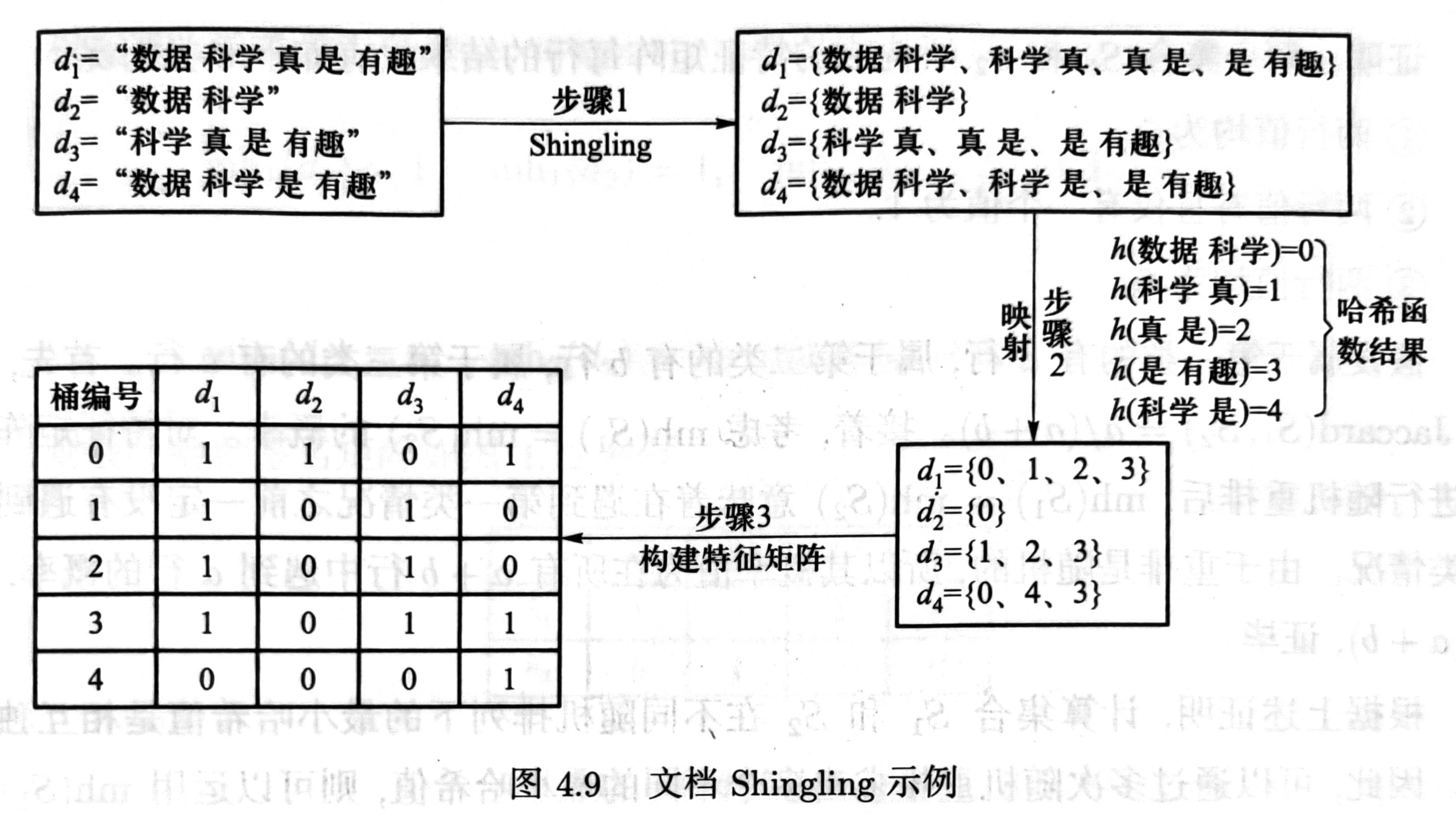
Shingling

将一篇文档视为一个字符串，文档的 $k$-Shingling 定义为其中任意长度为 $k$ 的字串。

这样每篇文档都可以用 $k$-Shingling 的集合或包来表示。（集合中的元素只能出现一次，包中的元素可以重复出现）

在得到某两篇文档的 Shingling 表示后，可用 Jaccard 距离来衡量两篇文档的相似度。

Jaccard 相似度

$$\text{Jaccard}(A, B) = \frac{A \cap B}{A \cup B}$$

Jaccard 距离

$$\text{DJ}(A, B) = 1 - \text{Jaccard}(A, B) = 1 - \frac{A \cap B}{A \cup B}$$

构建文档特征矩阵

Min-Hashing（最小哈希）

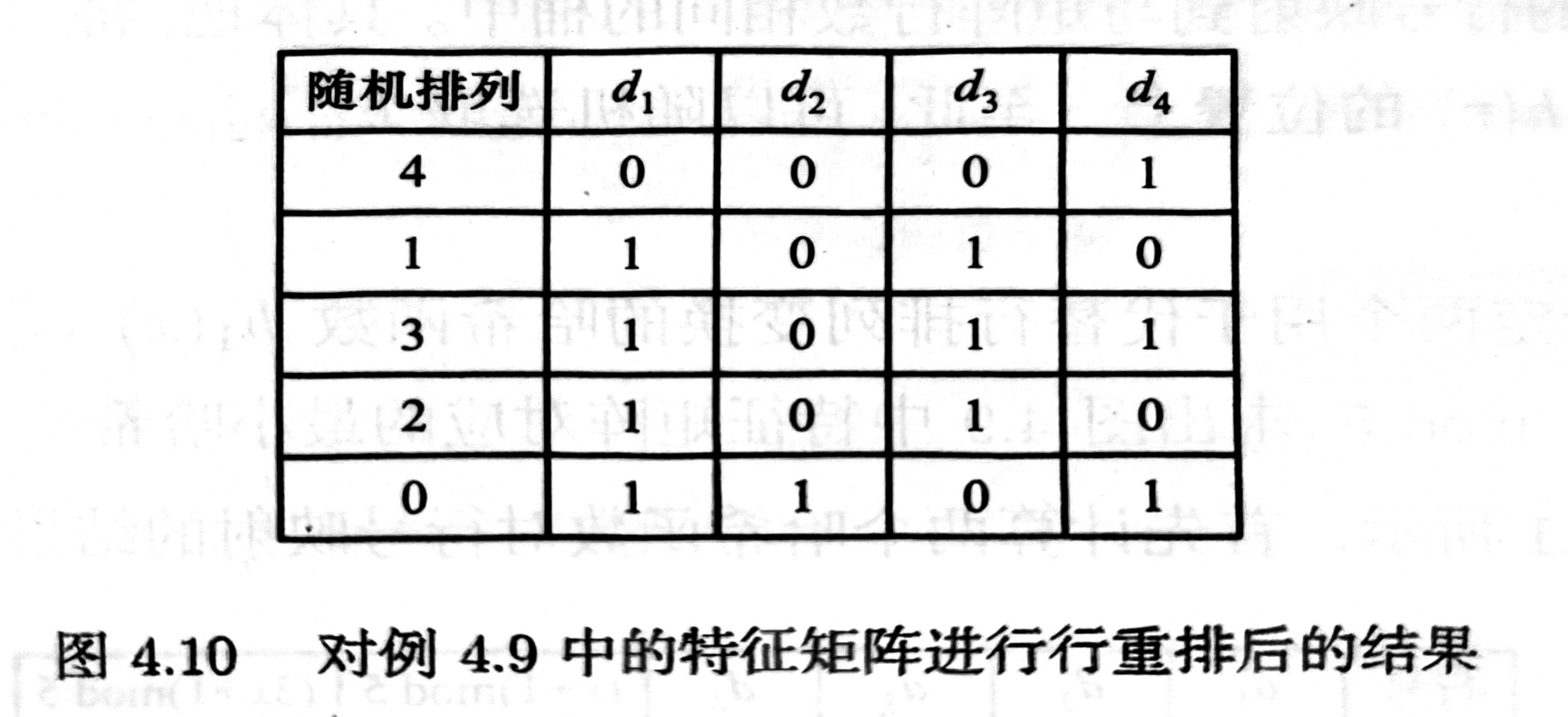
布尔向量 $v$，随机排列 $h$。$h(v)$ 为布尔向量经过随机排列后得到的新向量。$mh(v)$ 为新布尔向量中第一个不为 $0$ 的行号。

示例：$mh(d_1) = 0$，$mh(d_2) = 0$，$mh(d_3) = 1$，$mh(d_4) = 0$

定理1 ⭐

两个集合 $S_1$ 和 $S_2$ 经过多次随机排列之后得到的两个最小哈希值相等的概率，等于这两个集合的 Jaccard 相似度。

$$\text{Pr}[mh(S_1) = mh(S_2)] = \text{Jaccard}(S_1, S_2)$$

最小哈希签名

集合 $n$ 个最小哈希值构成的列向量即为 $S$ 的最小哈希签名。

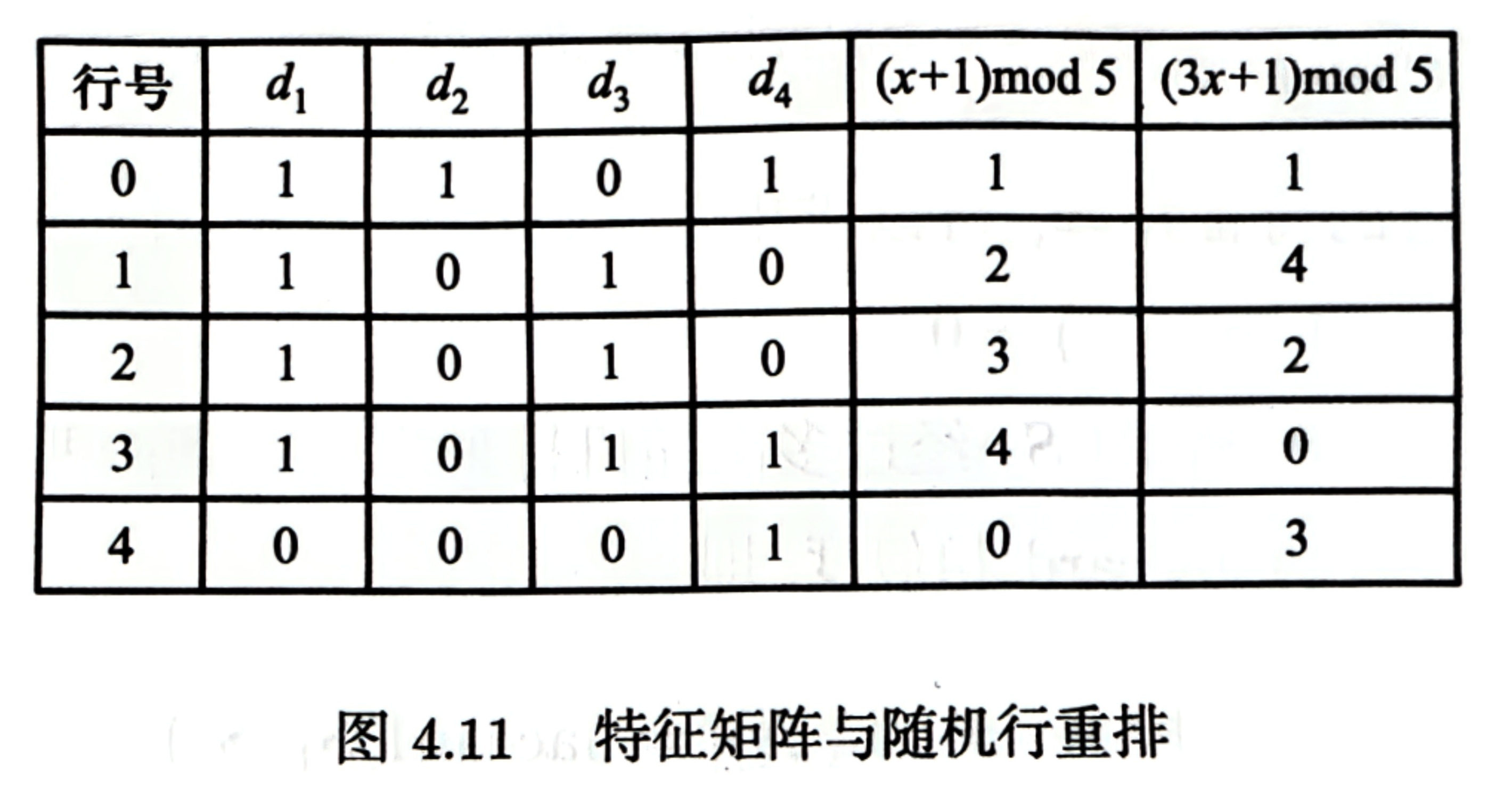
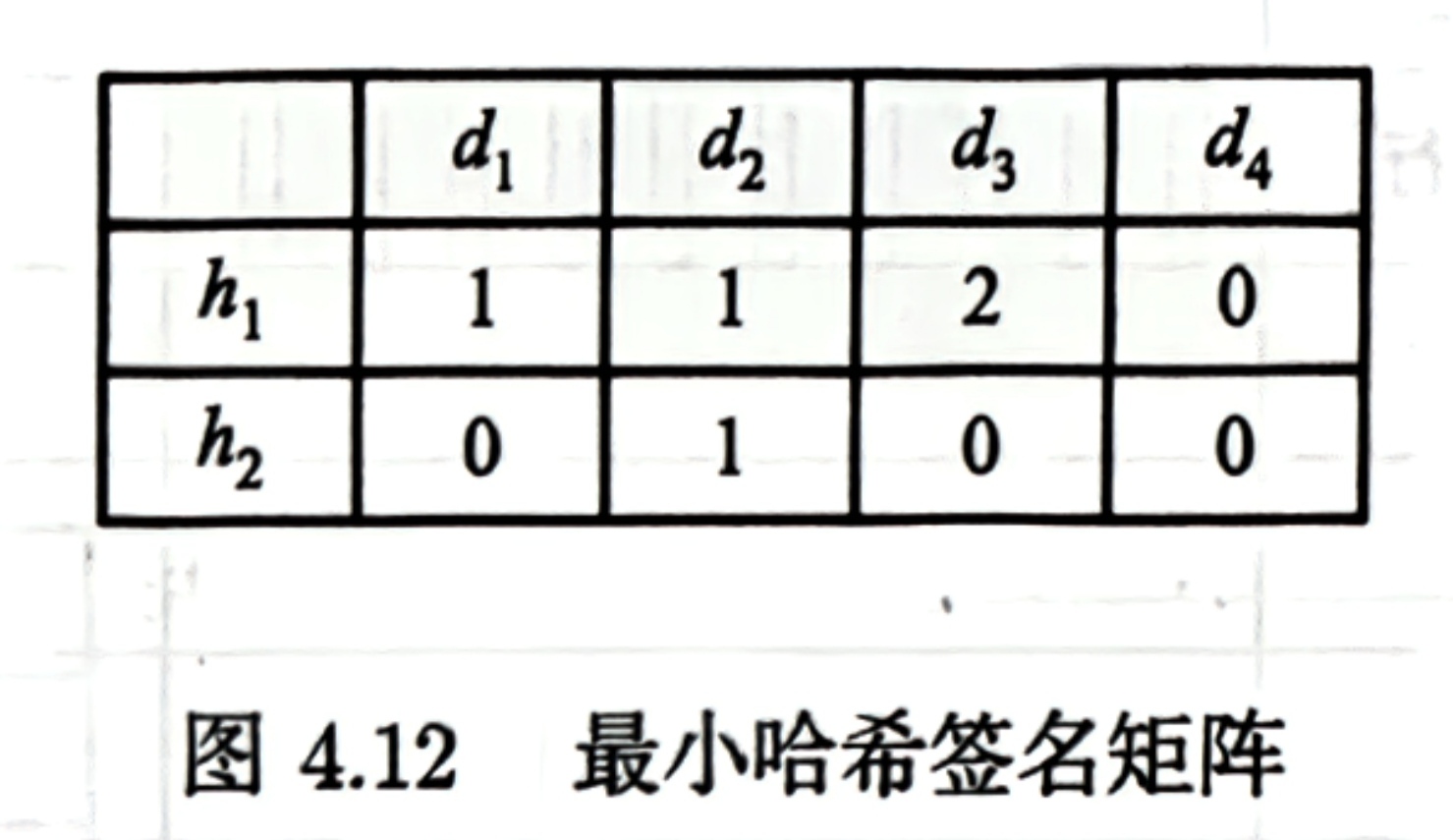
最小哈希签名矩阵

由多个集合的最小哈希签名构成的矩阵即为最小哈希签名矩阵。

最小哈希签名矩阵的相似度

基于最小哈希签名矩阵可以估算文档的相似度，但是当哈希函数个数较少时，估算误差可能会比较大。

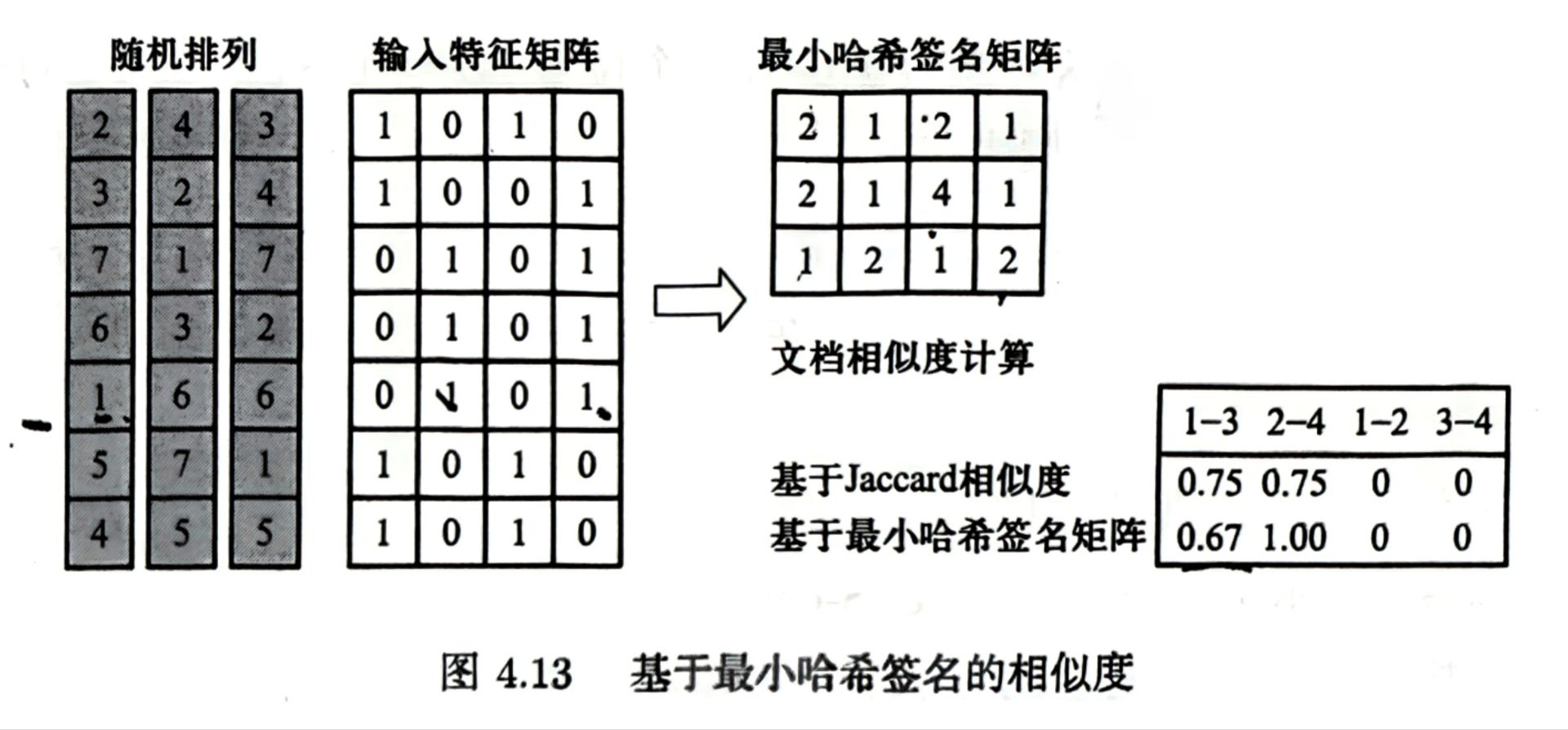
• 基于 Jaccard 相似度：通过“输入特征矩阵”使用 Jaccard 相似度计算。
• 基于最小哈希签名矩阵：通过“最小哈希签名矩阵”使用 Jaccard 相似度计算。

基于 Min-Hashing 的 LSH（局部敏感哈希）

得到最小哈希签名矩阵，就可以运用条块化方法实现局部敏感哈希（LSH）。

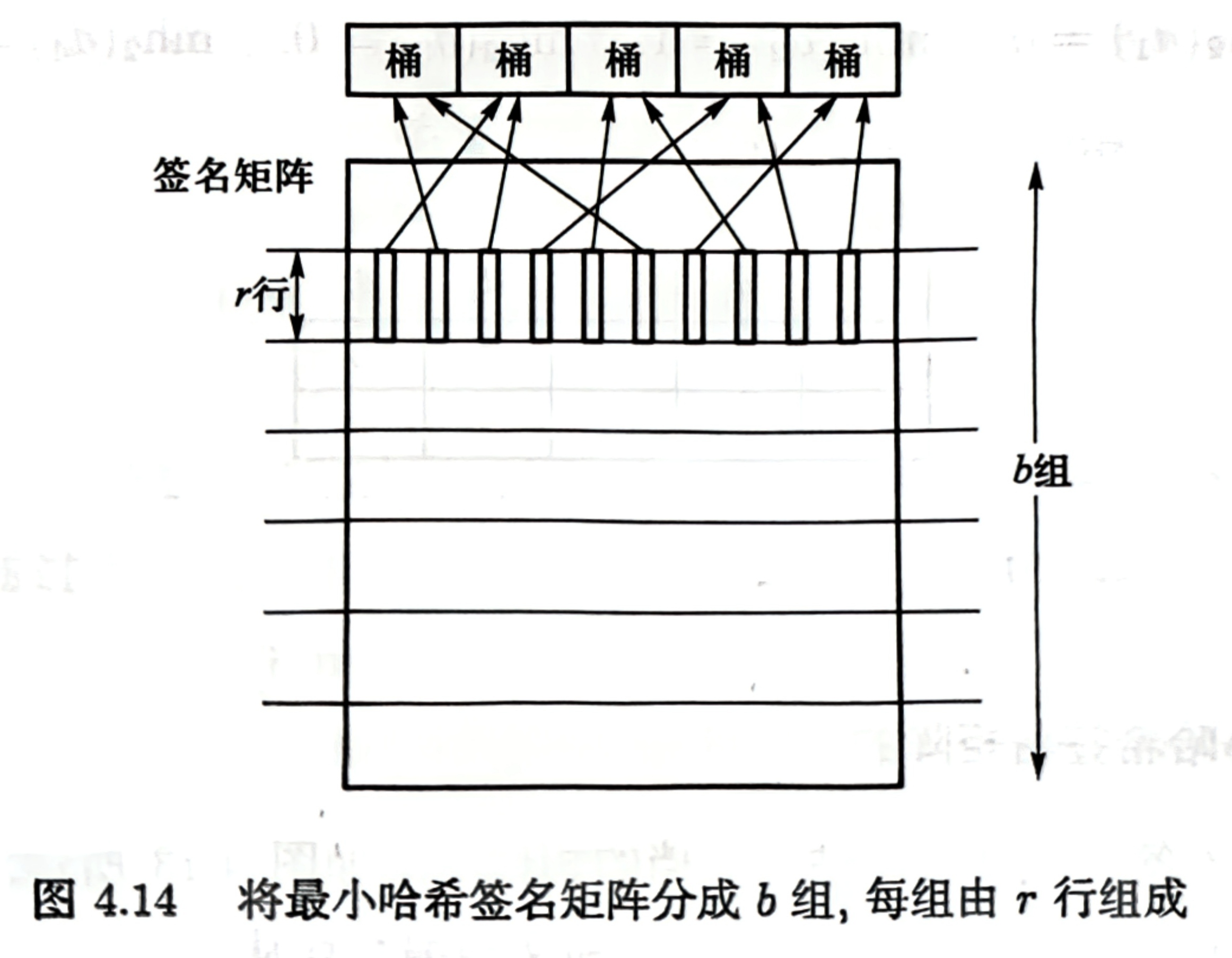
如图，将最小哈希签名矩阵划分为 $b$ 组或行条（band）。每组由 $r$ 行组成，都对应 $r$ 个哈希函数，由这 $r$ 个最小哈希组成的列向量决定一个集合映射到哪个桶中。

因此，$r$ 维列向量可以看作该集合的一个数字签名，拥有 $b$ 组意味着拥有 $b$ 次数字签名。两个集合只要有一个签名被映射到同一个桶中，就被认为是一对候选相似集合。

相似集合概率分析

假定将某个最小哈希签名矩阵划分为 $b$ 组，每组由 $r$ 行组成，两个集合 Jaccard 相似度为 $s$。由定理1可知，两个集合最小哈希相等的概率也为 $s$。那么两个集合被哈希到同一个桶中的概率与 Jaccard 相似度存在如下关系：

1. 在某个组中，两个集合最小哈希值相等的概率是 $s^r$。
2. 在某个组中，两个集合最小哈希值不相等的概率是 $1 - s^r$。
3. 在所有组中，两个集合最小哈希值都不相等的概率是 $(1 - s^r)^b$。
4. 在所有组中存在一个组满足，两个集合最小哈希值相等的概率是 $1 - (1 - s^r)^b$。

$1 - (1 - s^r)^b$ 即为使用 LSH 判定为相似集合的概率。