Merkov 不等式
X 为样本空间 Ω 上的非负随机变量,对任意一个正实数 a,都有:
其中 E(x) 为随机变量 X 的期望。
P(X≥a)≤aE(X) Chebyshev 不等式
其中 E(x) 和 Var(X) 分别为随机变量 X 的期望和方差。
X 为样本空间 Ω 上的随机变量,对任意一个正实数 r,都有:
P(∣X−E(X)∣≥r)≤r2Var(X) Chernoff 不等式
若 Xi 为定义在样本空间 Ω 上的 n 个独立伯努利随机变量,且 P(Xi=1)=pi。令 X=∑i=1nXi 和 μ=∑i=1npi,对任意小的 δ∈(0,1),则拥有两个结论:
P(X<(1−δ)μ)<exp(2−μδ2) P(X>(1+δ)μ)<exp(4−μδ2) Morris 与 Tug of War
Morris 算法
目的:当整数 n 非常大时,用更少的空间来近似表示整数 n。
算法流程:
- 更新操作:事件发生时,以 2X1 的概率更新 X 的值为 X+1,以 1−2X1 的概率保持 X 不变。
- 返回近似值 C:C=2X−1
缺陷:近似值的方差以二次多项式的形式在增加。
Morris+ 算法
优化点:通过多次取 Morris 算法的平均值可以获得波动更小的无偏估计。(可用 Chebyshev 不等式分析)
Morris+ 算法对事件的计数讲维护 n 个 Morris 计数器,返回的近似值是这 n 个计数的平均值。
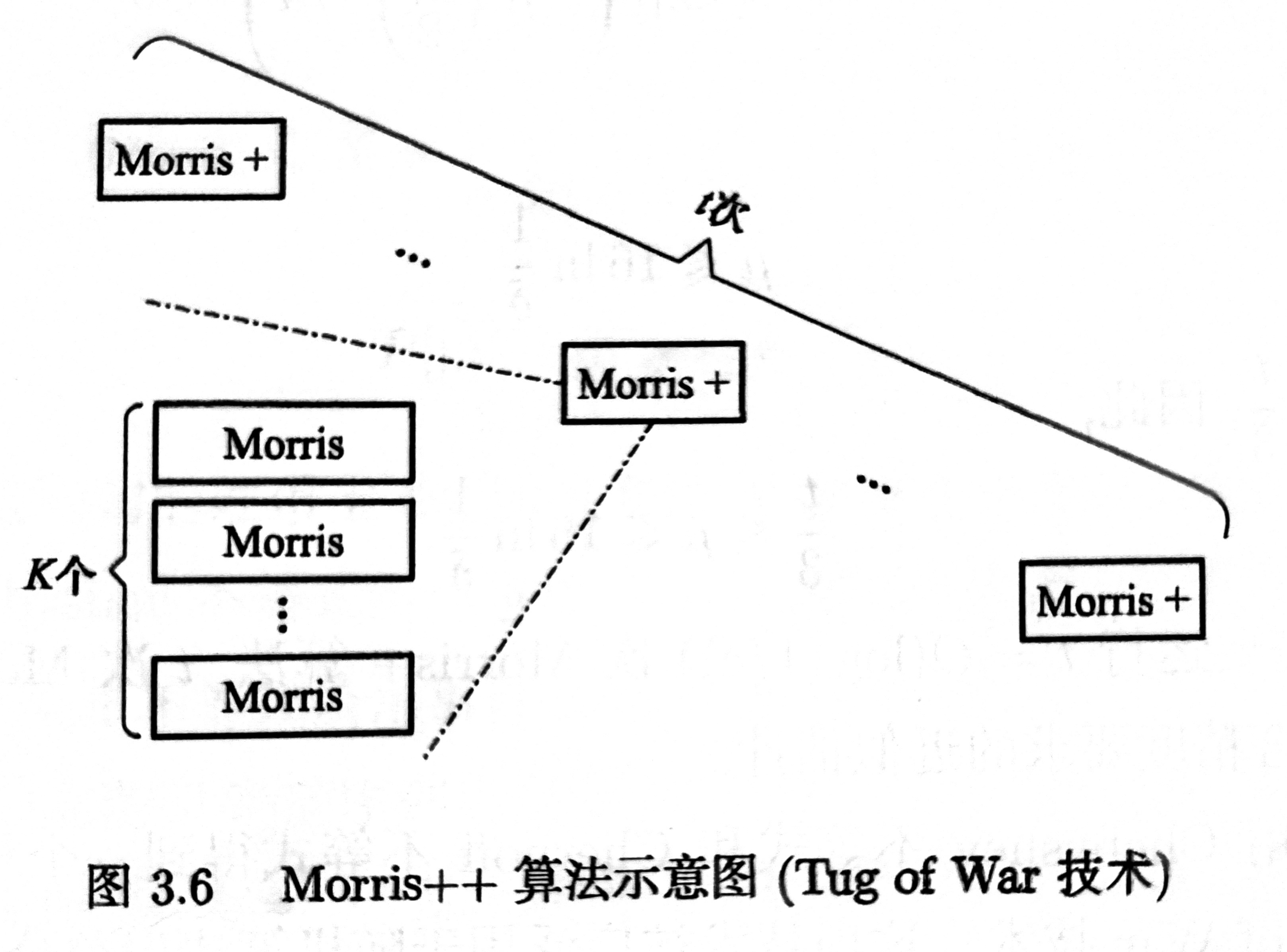
Morris++ 算法
通过多次取 Morris+ 算法的中位数可以获得波动更小的无偏估计。(可用 Chernoff 不等式分析)
Morris+ 算法运行 n=O(δϵ21) 次 Morris 算法,取 n 次输出平均值可用得到一个较好的近似估计。
优化点:Morris++ 算法只需要运行 n=O(ϵ2ln(1/δ)) 次 Morris 算法,就可以得到相同的精度。
Tug of War(拔河算法)
综合运用 Chebyshev 不等式和 Chernoff 不等式得到一个相对紧的概率上界的方法称为 Tug of War 技术。