For HDJ

向量和矩阵基础

注意

DJ 的行数是 $m$ ，列数是 $n$

$1 \times n$ 行向量， $m \times 1$ 列向量

实数：有理数和无理数的统称。实矩阵：矩阵 $A$ 中每一个元素都是实数。

复数：拥有实部和虚部 $a + bi$ 。复矩阵：矩阵 $A$ 中每一个元素都是复数。

向量的运算

向量之间的基本代数运算有两种：加法和数乘，统称为向量的线性运算。L2-[23-24]

矩阵的运算

矩阵的加法

两个相同 $m \times n$ 的矩阵相同位置上的元素相加， $C = (c_{ij})_{m \times n} = (a_{ij} + b_{ij})_{m \times n}$ 。L2-[25]

矩阵加法满足，交换律、结合律。L2-[26]

零矩阵 $O$

元素全为零的矩阵， $O_{m \times n}$ 。

矩阵相乘

$A = (a_{ij})_{m \times r}$ ， $B = (b_{ij})_{r \times n}$ ， $C = AB$ 。L2-[28]

矩阵相乘满足，结合律、左分配律、右分配律。不满足交换律。L2-[27]

单位矩阵

主对角线上的元素全是 $1$ , 其余元素全是 $0$ 的 $n$ 阶方阵。记为 $I$ 或 $I_n$ 。L2-[29]

矩阵和向量相乘

$Ax = b$ L2-[30]

矩阵和标量相乘

矩阵中的每一个元素都乘以标量值， $\lambda A = (\lambda a_{ij})_{m \times n}$ L2-[31]

矩阵分块

将大矩阵分为几个小矩阵，也满足矩阵的运算规律。L2-[34-35]

初等变换

一个非零的数，乘矩阵的某一行（列）
把矩阵的某一行（列）的 $c$ 倍加到另一行（列）
交换两行（列）的位置

行变换相当于左乘初等矩阵，列变换相当于右乘初等矩阵。L2-[37]

可逆矩阵

$AA^{-1} = I$ ，则 $A$ 可逆。称为“可逆”、“正规”、“非奇异”的。

“奇异” = “不可逆”

如果它可逆，我们就能通过初等行变换求出它的可逆矩阵。L2-[39]

转置矩阵

行和列互换， $A^T = (a_{ji})_{n \times m}$

逆和转置的性质

$AA^{-1} = A^{-1}A = I$
$(A+B)^{-1} \neq A^{-1} + B^{-1}$
$(A+B)^T = A^T + B^T$
$(AB)^{-1} = B^{-1}A^{-1}$
$(AB)^T = B^TA^T$
$(A^{-1})^T = (A^T)^{-1}$

利用初等行变换求解线性方程组

先画出增广矩阵，将系数矩阵化成单位阵，此时右边一列即为方程组的解。L2-[44]

利用系数矩阵的逆矩阵求解线性方程组

$A^{-1}Ax=A^{-1}b$ ，那么 $Ix = A^{-1}b$ ，即 $x = A^{-1}b$ 。L2-[45]

向量空间

又称为“线性空间”。在这个空间上，向量以及向量的运算，共同构造出的空间。（但实际上，数或矩阵的空间也叫向量空间）L3-[4]

设 $\mathbb{V}$ 是 $n$ 维向量的非空集合， $\mathbb{K}$ 是数域。

$\mathbb{V}$ 上定义了加法
$\mathbb{K}$ 与集合 $\mathbb{V}$ 定义了数乘
$\forall a, b \in \mathbb{V}$ ，都有任意的 $k \in \mathbb{K}$ ，满足 $a + b, ka \in \mathbb{V}$ 。（加法和数乘运算封闭）

满足上面三条，称 $\mathbb{V}$ 为数域 $\mathbb{K}$ 上的 $n$ 维向量空间或线性空间。L3-[6]

所以有例1和例2的向量空间、矩阵空间。L3-[7-8]。例3复数域的向量空间、例4一元多项式的向量空间。L3-[8-10]

向量子空间

设 $\mathbb{X}$ 是 $\mathbb{K}$ 上的 $n$ 维线性空间， $\mathbb{Y}$ 是 $\mathbb{X}$ 的子集。如果满足：（加法和数乘运算封闭）

若 $x, y \in \mathbb{Y}$ , 则 $x + y \in \mathbb{Y}$
若 $a \in \mathbb{K}$ ， $x \in \mathbb{Y}$ ，则 $ax \in \mathbb{Y}$

则称 $\mathbb{Y}$ 是 $\mathbb{X}$ 的线性子空间，简称子空间。L3-[12]

非空的线性空间一定会有的子空间：自身和 ${0}$

零子空间

只含零向量的子集称为零子空间。L3-[12]

平凡子空间

零子空间、线性空间本身统称为平凡子空间，其他子空间称为非平凡子空间。L3-[12]

二维实数子空间 $\mathbb{R}^2$

$\mathbb{R}^2$ 空间指二维空间。下图中，只有 $D$ 是 $\mathbb{R}^2$ 的子空间。L3-[13]

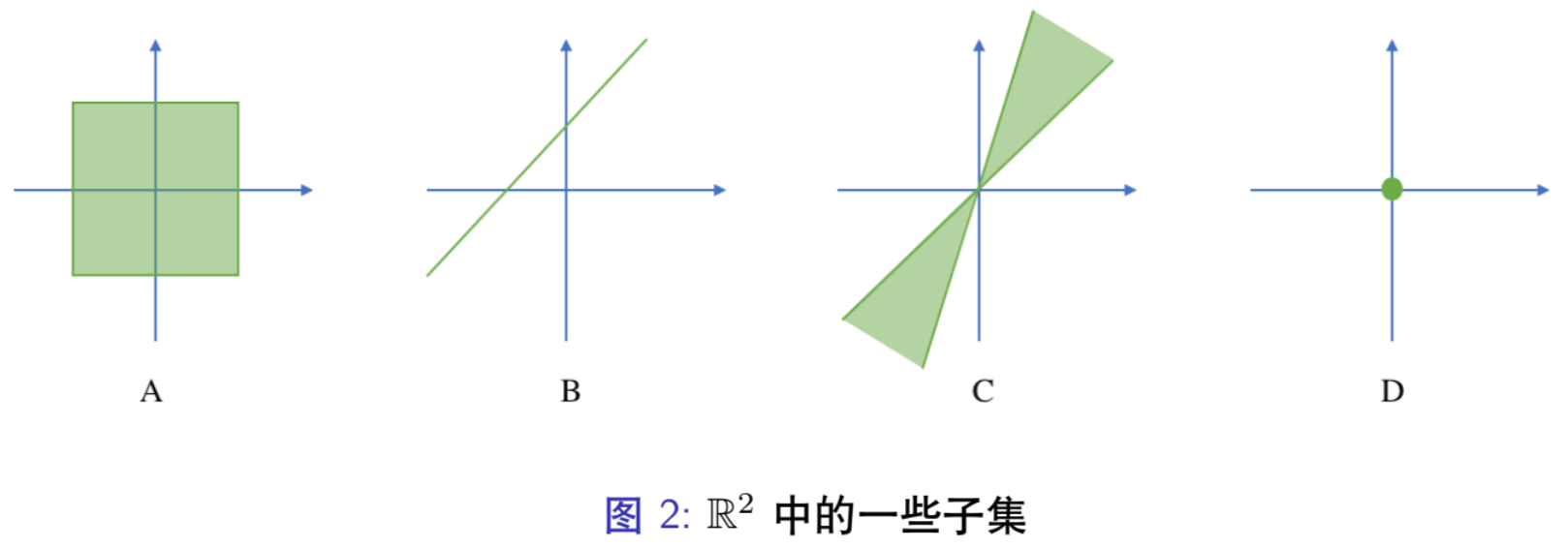
子空间的证明

知乎：如何证明一个向量空间是另一个向量空间的子空间？

子集
加法零元
加法运算封闭
数乘运算封闭

线性方程组 $Ax = b$ 的解空间

L3-[14]

子空间的交、和、直和

前提： $\mathbb{Y}_1$ 和 $\mathbb{Y}_2$ 均为 $\mathbb{X}$ 的子空间。L3-[15-16]

交

若用 $\mathbb{Y}_1 \cap \mathbb{Y}_2$ 表示集合的交集，则 $\mathbb{Y}_1 \cap \mathbb{Y}_2$ 也是 $\mathbb{X}$ 的子空间。称为“交”

和

若用 $\mathbb{Y}_1 + \mathbb{Y}_2$ 表示 $y_1 + y_2 (y_1 \in \mathbb{Y}_1, y_2 \in \mathbb{Y}_2)$ 组成的集合，则 $\mathbb{Y}_1 + \mathbb{Y}_2$ 也是 $\mathbb{X}$ 的子空间。称为“和”。

直和

若 $\mathbb{Y}$ 每个向量 $x$ 可唯一表示成 $x = y_1 + y_2 (y_1 \in \mathbb{Y}_1, y_2 \in \mathbb{Y}_2)$ 。则称 $\mathbb{Y}$ 为 $\mathbb{Y}_1$ 与 $\mathbb{Y}_2$ 的“直和”。记为 $\mathbb{Y} = \mathbb{Y}_1 + \mathbb{Y}_2$ 或 $\mathbb{Y} = \mathbb{Y}_1 \oplus \mathbb{Y}_2$

定理3和定理4，为直和的充要条件。L3-[16]

线性无关性

线性组合、组合系数、线性表出

设向量 $a_1$ , $a_2$ , ..., $a_s$ 是数域上 $\mathbb{K}$ 上的 $n$ 维向量组。
设一组数 $k_1$ , $k_2$ , ..., $k_s$ 在数域上 $\mathbb{K}$ 。

那么表达式 $k_1a_1 + k_2a_2 + ... + k_sa_s$ 称为向量组 $a_1$ , $a_2$ , ..., $a_s$ 的一个线性组合。 $k_1$ , $k_2$ , ..., $k_s$ 称为组合系数。

若向量 $b$ 是向量组 $a_1$ , $a_2$ , ..., $a_s$ 一个线性组合，即 $b = k_1a_1 + k_2a_2 + ... + k_sa_s$ ，则称 $b$ 可以由向量组 $a_1$ , $a_2$ , ..., $a_s$ 线性表出。L3-[19-20]

线性相关、线性无关

可以看 PPT 的 23 页 L3-[23]。

解方程 $k_1a_1 + k_2a_2 = 0$ ，当且仅当 $k_1 = k_2 = 0$ 时成立。L3-[32]

极大线性无关组

向量组的一部分组称为一个极大线性无关组, 如果这个部分组本身线性无关，但从原向量组的其余向量中任取一个添加进去后，所得的部分组都线性相关。L3-[21-23]

等价向量组

如果向量组 $a_1$ , $a_2$ , ..., $a_s$ 每一个向量都可以用 $b_1$ , $b_2$ , ..., $b_t$ 线性表出，则称向量组 $a_1$ , $a_2$ , ..., $a_s$ 可以用 $b_1$ , $b_2$ , ..., $b_t$ 线性表出。

如果两个向量组可以线性表出，则称它们等价。L3-[25]

生成集

设 $a_1$ , $a_2$ , ..., $a_r$ 是 $\mathbb{V}$ 的一组向量，这组向量所有可能的线性组合所成的集合是 $\mathbb{V}$ 的一个子空间。该子空间称为由 $a_1$ , $a_2$ , ..., $a_r$ 张成的子空间，记作 $L(a_1$ , $a_2$ , ..., $a_r)$ 或 $span(a_1$ , $a_2$ , ..., $a_r)$ 。那么 $\{a_1, a_2, ..., a_r\}$ 就叫做 $\mathbb{V}$ 的一个生成集。L3-[27]

两个向量组张成相同子空间的充要条件是：两个向量组等价。

维数、基

如果向量空间 $\mathbb{V}$ 中由 $n$ 个线性无关的向量 $a_1$ , $a_2$ , ..., $a_n$ ，且 $\mathbb{V}$ 中任一向量都可以用它们线性表出，则称 $\mathbb{V}$ 为 $\mathbb{K}$ 上的 $n$ 维线性空间。

那么， $n$ 称为 $\mathbb{V}$ 的维数。记作 $dim(\mathbb{V}) = n$ 。而 $a_1$ , $a_2$ , ..., $a_n$ 就是 $\mathbb{V}$ 的一组基。

一些关于基、最小生成集、极大线性无关组的等价命题L3-[30]：令 $\mathbb{V}$ 是一向量空间， $\mathbb{B} \subseteq \mathbb{V}$ ， $\mathbb{B} \neq \empty$ ，下面命题等价：

$\mathbb{B}$ 是 $\mathbb{V}$ 的一个基
$\mathbb{B}$ 是最小生成集
$\mathbb{B}$ 是 $\mathbb{V}$ 中的极大线性无关组
$\mathbb{V}$ 中的每一个向量能被 $\mathbb{B}$ 线性表出

标准基

如果一组基中的每一个向量长度均为 $1$ ，我们称其为标准基。L3-[31]

确定向量组是否是一组基

求解极大线性无关组，有多少个线性无关的向量就是几维向量空间。L3-[32-33]

子空间的扩张

L3-[34]

假设有 $n$ 维空间 $\mathbb{X}$ ，它有一个 $m$ 维子空间 $\mathbb{Y} = L(a_1, a_2, ..., a_m)$ ，这个向量组可以扩张为 $a_1, a_2, ..., a_m, a_{m+1}, ..., a_n$ ，使得 $\mathbb{X} = L(a_1, a_2, ..., a_m, a_{m+1}, ..., a_n)$

L(a_1, a_2, ..., a_m) \oplus L(a_{m+1}, ..., a_n)= L(a_1, a_2, ..., a_m, a_{m+1}, ..., a_n)

那么就有一些和、直和维数公式。

$dim(\mathbb{Y}_1 + \mathbb{Y}_2) = dim \mathbb{Y}_1 + dim\mathbb{Y}_2 - dim(\mathbb{Y}_1 \cap \mathbb{Y}_2)$
$dim(\mathbb{Y}_1 \oplus \mathbb{Y}_2) = dim \mathbb{Y}_1 + \mathbb{Y}_2$

有限维线性空间

如果向量空间 $\mathbb{V}$ 中任一向量都能被 $n$ 个线性无关的向量线性表出时， $\mathbb{V}$ 称为有限维线性空间。否则称为无限维线性空间。L3-[35]

坐标

一个向量被一组基“线性表出”的系数。

在 $n$ 维向量空间 $\mathbb{V}$ 中， $n$ 个线性无关的向量 $\epsilon_1, \epsilon_2, ..., \epsilon_n$ 称为 $\mathbb{V}$ 的一组基。设 $a$ 是 $\mathbb{V}$ 中的任一向量，那么肯定 $\epsilon_1, \epsilon_2, ..., \epsilon_n, a$ 线性相关。因此 $a$ 可以被基 $\epsilon_1, \epsilon_2, ..., \epsilon_n$ 线性表出：

a = a_1\epsilon_1 + a_2\epsilon_2 + ... + a_n\epsilon_n

这系数就成为 $a$ 在基 $\epsilon_1, \epsilon_2, ..., \epsilon_n$ 下的坐标，记为 $(a_1, a_2, ..., a_n)$ 。L3-[36]

例15：有关泰勒展开的例子 L3-[37]，例16：换基之后的坐标 L3-[39]

秩

极大线性无关组中所含向量的个数称为这个这个向量组的秩，记作 $rank\{a_1, a_2, ..., a_r\}$

$dim L(a_1, a_2, ..., a_r) = rank\{a_1, a_2, ..., a_r\}$ 维数和秩相等。

矩阵的秩有行向量的行秩，和列向量的列秩，它们都相等，都称为矩阵的秩，记作 $rank(A)$ 。

可以看例17。L3-[43]

仿射子空间

令 $\mathbb{V}$ 是一线性空间， $x_0 \in \mathbb{V}$ ，且 $\mathbb{U} \subseteq \mathbb{V}$ 是一线性子空间，则子集 $\mathbb{L} = x_0 + \mathbb{U} := \{x_0 + u | u \in \mathbb{U}\} \subseteq \mathbb{U}$ 是一仿射子空间。

我们定义线性子空间的维数是仿射子空间的维数。

若 $\mathbb{U}$ 有一基底 $a_1, a_2, ..., a_m$ ，则 $\mathbb{L}$ 中的每一个元素 $x$ 均可写成 $x_0 + k_1a_1 + k_2a_2 + ... + k_ma_m$ 。L3-[48]

超平面

$\mathbb{R}^3$ 的 $n-1$ 维仿射子空间称为超平面。例如三维空间中一个平面就是它的超平面，四维空间中，一个超平面是三维空间。L3-[49]

$Ax=b, b \neq 0$ 的解空间是一个仿射空间

L3-[50]

线性映射

集合的映射

L4-[5]

设 $\mathbb{V}$ ， $\mathbb{W}$ 是两个非空集合，如果存在一个映射 $f$ ，使得对 $\mathbb{V}$ 中每个元素 $v$ ，在 $\mathbb{W}$ 中有唯一确定的元素 $w$ 与之对应，则称 $f$ 为从 $\mathbb{V}$ 到 $\mathbb{W}$ 的映射，记作：

f: \mathbb{V} \rightarrow \mathbb{W}

$w$ 称为元素 $v$ 在映射 $f$ 下的像，并记作 $f(v)$ ，即 $w = f(v)$ 。
$v$ 称为元素 $w$ 在映射 $f$ 下的原像。
集合 $\mathbb{V}$ 称为映射 $f$ 的定义域，记作 $D_f$ 。即 $D_f = v$ 。
$\mathbb{V}$ 中所有元素的像所组成的集合称为映射 $f$ 的值域，记作 $R_f$ 或 $f(\mathbb{V})$ 。即 $R_f = f(\mathbb{V})=\{f(v) | v \in \mathbb{V}\}$ 。

单射、满射、双射

L4-[6]

设 $\mathbb{V}$ ， $\mathbb{W}$ 是任意两个集合， $\varphi: \mathbb{V} \rightarrow \mathbb{W}$ 是一个映射，如果

$\forall x, y \in \mathbb{V}$ ，若 $\varphi(x) = \varphi(y)$ ，一定是 $x = y$ ，则称 $\varphi$ 为单射。
$\varphi(\mathbb{V}) = \mathbb{W}$ ，则称 $\varphi$ 为满射。
如果既是单射又是满射，则称 $\varphi$ 为双射。

线性映射

L4-[7]

设 $\mathbb{V}$ ， $\mathbb{W}$ 是数域 $K$ 上的两个有限维的向量空间， $\varphi$ 是 $\mathbb{V}$ 到 $\mathbb{W}$ 的一个映射。

如果对任何向量 $x, y \in \mathbb{V}$ 及任意的 $\alpha, \beta \in \mathbb{K}$ 都满足下式，则称 $\varphi$ 是 $\mathbb{V}$ 到 $\mathbb{W}$ 的一个线性映射。

\varphi (\alpha x+\beta y) = \alpha \varphi (x) + \beta \varphi (y)

一个满足线性映射的例子：L4-[10]

一个不满足线性映射的例子：L4-[9]。

恒等映射

L4-[8]

若映射 $\sigma : \mathbb{V} \rightarrow \mathbb{V}$ ， $\sigma (x) = x$ ，那么它就是一个恒等映射。

$\sigma (\alpha x + \beta y) = \alpha x + \beta y = \alpha \sigma (x) + \beta \sigma (y)$ 。
恒等映射也是线性映射。

向量空间之间的特殊映射

L4-[11]

设 $\mathbb{V}$ ， $\mathbb{W}$ 是数域 $\mathbb{K}$ 上的两个有限维的向量空间：

$\varphi : \mathbb{V} \rightarrow \mathbb{W}$ 是线性映射，则 $\mathbb{V}$ ， $\mathbb{W}$ 同态。 $\varphi$ 称为同态映射。
$\varphi : \mathbb{V} \rightarrow \mathbb{W}$ 是线性映射且是双射，则则 $\mathbb{V}$ ， $\mathbb{W}$ 同构。 $\varphi$ 称为同构映射。
$\varphi : \mathbb{V} \rightarrow \mathbb{V}$ 是线性映射，则 $\mathbb{V}$ 自同态。 $\varphi$ 称为自同态映射。
$\varphi : \mathbb{V} \rightarrow \mathbb{V}$ 是线性映射且是双射，则 $\mathbb{V}$ 自同构。 $\varphi$ 称为自同构映射。

若 $\mathbb{V}$ ， $\mathbb{W}$ 同构，当且仅当 $dim(\mathbb{X}_1) = dim(\mathbb{X}_2)$ L4-[13]

逆映射

如果 $\varphi : \mathbb{V} \rightarrow \mathbb{W}$ 是一个双射，则可以定义它的逆映射，记作 $\varphi^{-1} : \mathbb{W} \rightarrow \mathbb{V}$ 。 L4-[14]

向量空间映射的运算

考虑向量空间 $\mathbb{V}$ ， $\mathbb{W}$ ， $\mathbb{X}$ ，则有：L4-[15]

对于线性映射 $\varphi : \mathbb{V} \rightarrow \mathbb{W}$ 和 $\phi : \mathbb{W} \rightarrow \mathbb{X}$ ，则 $\phi (\varphi)$ 也是一个线性映射。
如果 $\varphi : \mathbb{V} \rightarrow \mathbb{W}$ 是同构映射，则 $\varphi^{-1} : \mathbb{W} \rightarrow \mathbb{V}$ 也是一个同构映射。
如果 $\varphi : \mathbb{V} \rightarrow \mathbb{W}$ 和 $\phi : \mathbb{V} \rightarrow \mathbb{W}$ 是线性映射，且 $\lambda \in \mathbb{R}$ ，则 $\varphi + \phi$ 和 $\lambda \varphi$ 也是线性映射。

线性映射的矩阵表示

考虑一个 $n$ 维向量空间 $\mathbb{V}$ 的基底 $\{b_1, ..., b_n\}$ ，并为基向量规定一个顺序。如果基底有序，则称其为有序基。L4-[19]

使用不同的基表示同一坐标

例子：L4-[21]

变换矩阵

例子：L4-[24]

变换矩阵的求解

基变换

反正目前我看不懂：L4-[25-28]

矩阵等价

如果对于两个矩阵 $A, B \in \mathbb{R}^{m \times n}$ ，存在可逆矩阵 $S \in \mathbb{R}^{n \times n}$ ， $T \in \mathbb{R}^{m \times m}$ 使得 $A = T^{-1}BS$ 成立，则称 $A, B$ 等价。